Neural Networks as Linear Combinations.
• NNs are multiple linear methods working in combination, but the power of non-linearity is what makes the difference.
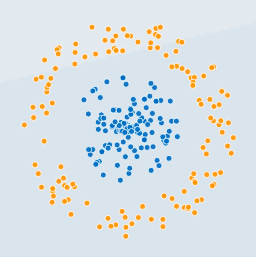
• Let's see how many lines it'd take you to separate these two groups?
↓
• At first we can try to see how a single line does.
• This is something a logistic regression with linear function would do.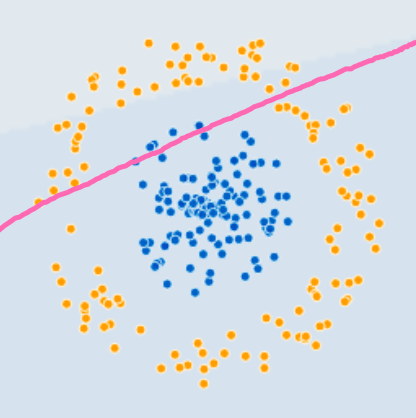
• As expected there isn't much that can be done with it.
• Without worrying about the activation function let's try using a NN.
• With one neuron in the hidden layer, it can be thought of as common logistic regression.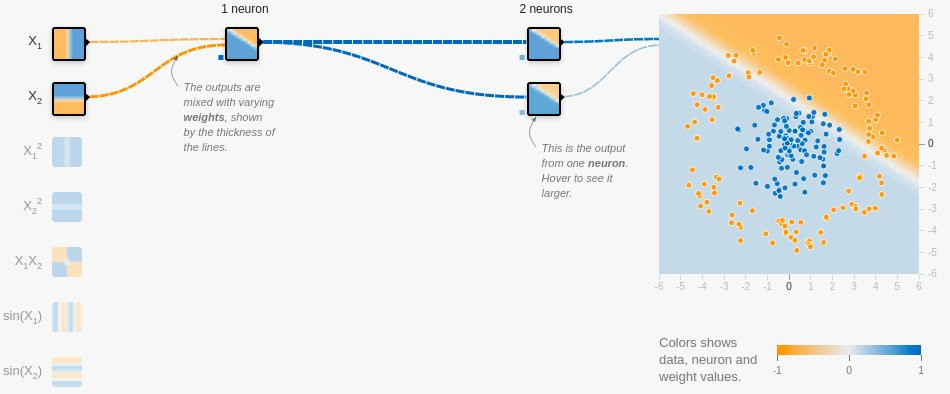
• Now we can increase the number of lines to solve the problem.
• Trying it with two lines now is expected to give a better solution.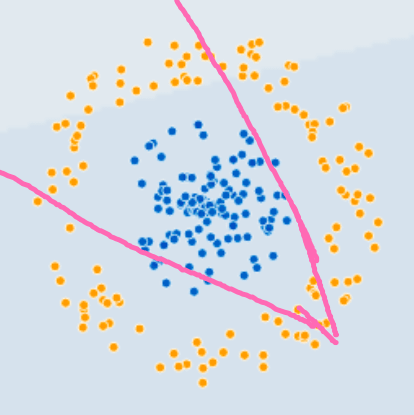
• Much better than a single line but we're still misclassifying some of the orange observations as well.
• Let's check with NN having two neurons.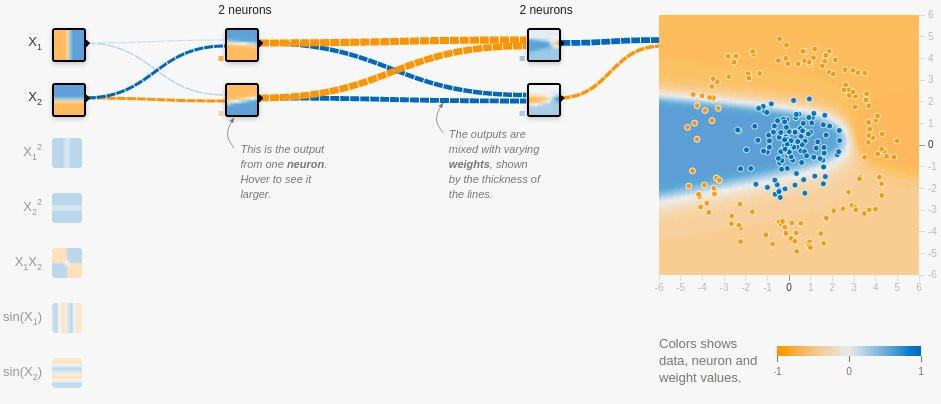
• As expected, not a perfect solution. What about three lines? Would that work?
• It could. Let's try. Seem possible.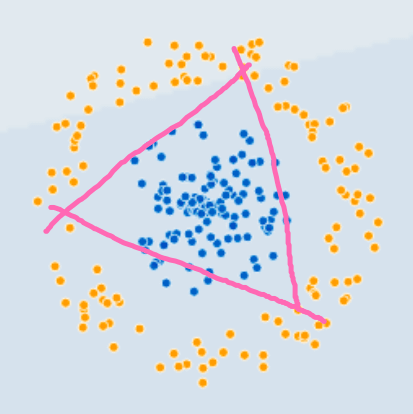
• Now increase the neurons to three.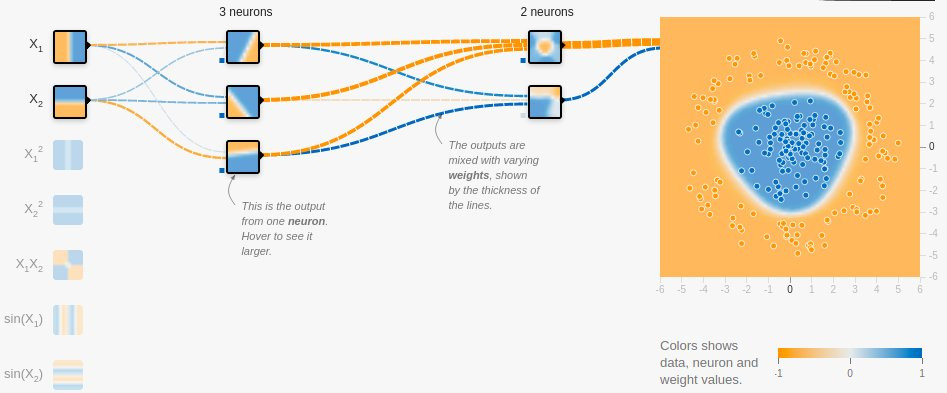
• It is quite evident that we can do it with 3 neurons which is analogous to using 3 lines.
• So a neural network is a combination of linear methods BUT non-linearity is playing a key role here.
• All the outputs of the neurons are mapped to a continuous non-linear function that allows the complex learning and backpropagation to work.
• What would happen if we just apply the linear activation and not apply any activation at all?
• A combination of linear systems yields only another linear system,
• Without the non-linear activations the model would only try to fit a new single line to it, which we know won't work.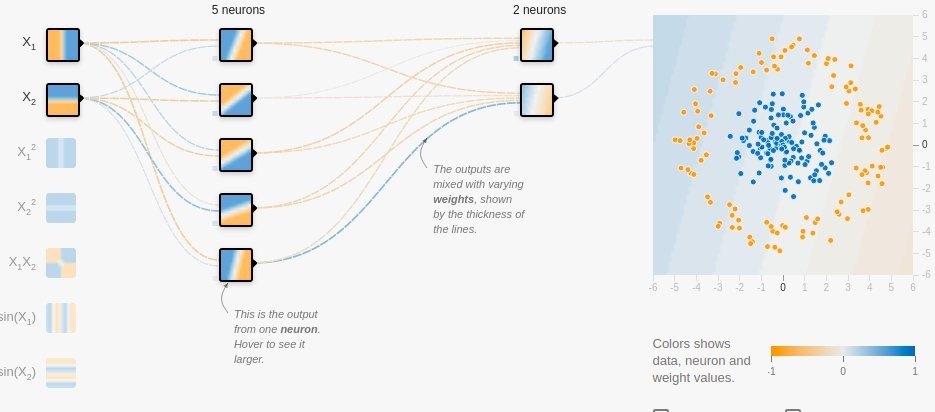
• We are trying to estimate an unknown function that can't always be approximated by simple linear functions,
• That is why we add non-linear transformations to the inputs.
If you're intrigued, do mess around with the architecture using the playground.
This helps in building good intuition.
playground.tensorflow.com