🧵 What is a zero-knowledge proof [system]?
It's the *sane* way of proving a statement is true.
For example, say I want to convince you I can solve a Sudoku puzzle *x*.
Why should I have to give you the solution *w* to the puzzle? You did not ask me for the solution, did you?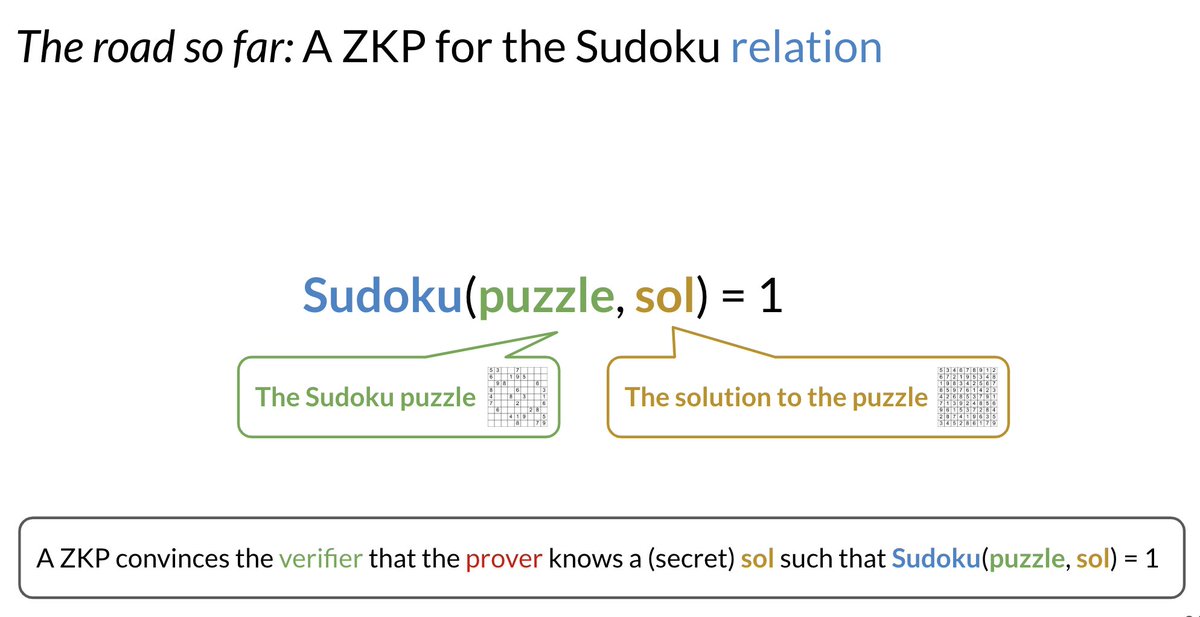
You asked me to convince you I can solve the puzzle! Those are very different asks.
Isn't it a bit *insane* for me to give you the solution *w* if you only want to be convinced I can solve the puzzle?
The difficulty is we're used to this *insanity*, both on the web & in society
For example, we assume a website must be given a user's password as a proof that the user knows the password. Nonsense.
Or, we assume that an identity verifier must be given a person's social security # as a proof that they have been issued that #. (Dangerous) nonsense, which...
...unfortunately leads to identity theft.
This *insane* way of proving a statement by giving you all this extra, often sensitive, information is (part of) what ZKPs solve.
To keep this tweetstorm short, here's a ZKP of a Sudoku solution (and more): docs.google.com/presentation/d/1b2FoHN983iA_ZkiISMCKa0JqlE40CeqaqNxWjWiJQjE/edit?usp=sharing
In general, a ZKP for an *algorithm* *R* enables a *prover* to convince a *verifier* that the prover knows a secret *w* such that *R(x, w) = 1*, where *x* is known by both the prover & the verifier.
A bit of a tedious/boring abstraction... what is this *R*? Let's talk alcohol...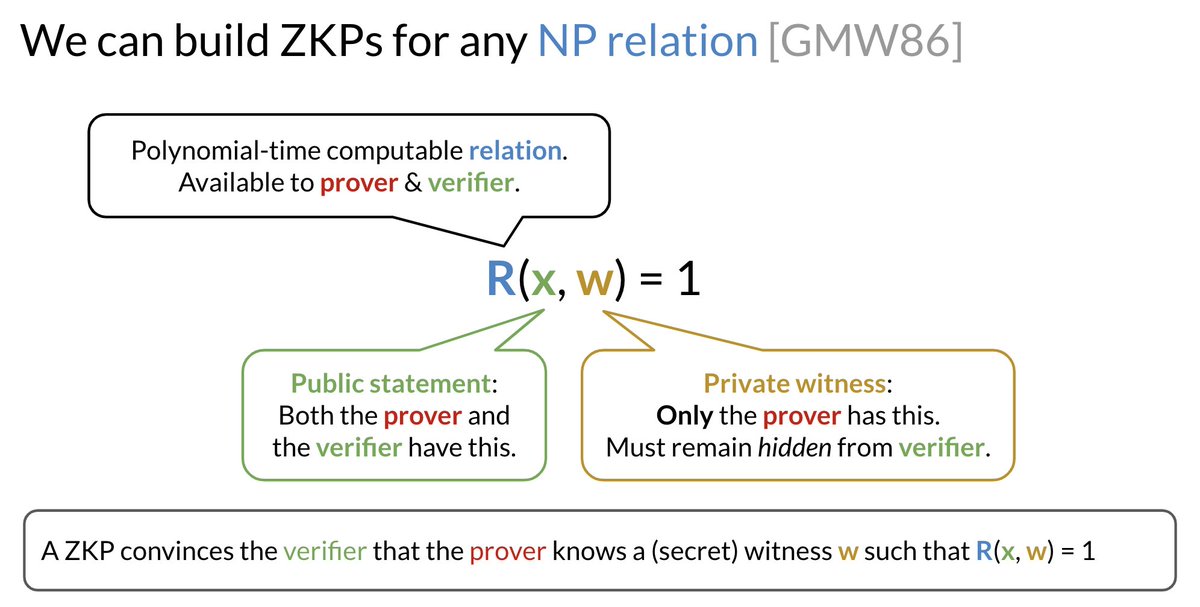
You are the *prover*. You have an ID card, which includes your date of birth (DOB) & is digitally-signed by your government.
The bar is the *verifier*.
They want to check that their `R = CanDrink` age verification algorithm succeeds: i.e., you are of drinking age.
On the other hand, you want to hide your name & DoB from the bar.
The bar only has the current date & the PK under which your ID is signed.
You compute a ZKP for the `CanDrink` algorithm, which (1) checks your ID's signature, (2) checks your age given the current date.
Most importantly, this ZKP hides your secrets: i.e., your name, DoB & the digital signature on your ID (which leaks name+DoB via bruteforcing).
The bar verifies this ZKP only against the current date & the PK.
The bar is *only* convinced that you *have* a valid ID & are of age.
Remember: The *sane* way is to *just* convince the bar that you can drink, without *insanely* leaking your name and DoB which, if done electronically, would leave a potentially-embarrassing trail of the (little) drinking you've been doing to all of your Eastern European friends.
ZKPs do more than maintain secrecy of the witness *w* when you prove that R(x, w) = 1.
1. They can have an extremely *succinct* proof (even though *x* and *w* might be large)
2. They can be much faster to verify than re-executing *R(x, w)* itself
This opens many other applications.
Let's do a complicated example of a (non-ZK)P, where the ZK property is not needed, but the succinctness of the proof & the fast verification is (points 1 & 2 from above).
This assumes familiarity with Merkle trees and/or state commitments.
e.g., rollups for L2s for payments!
Here, the L1 should verify that a block of L2 payment TXNs were valid, updating an old Merkle root of the L2 state to a new one.
The L1 (i.e., the *verifier*) has the old & new Merkle roots and the block of TXNs (i.e., the statement *x*)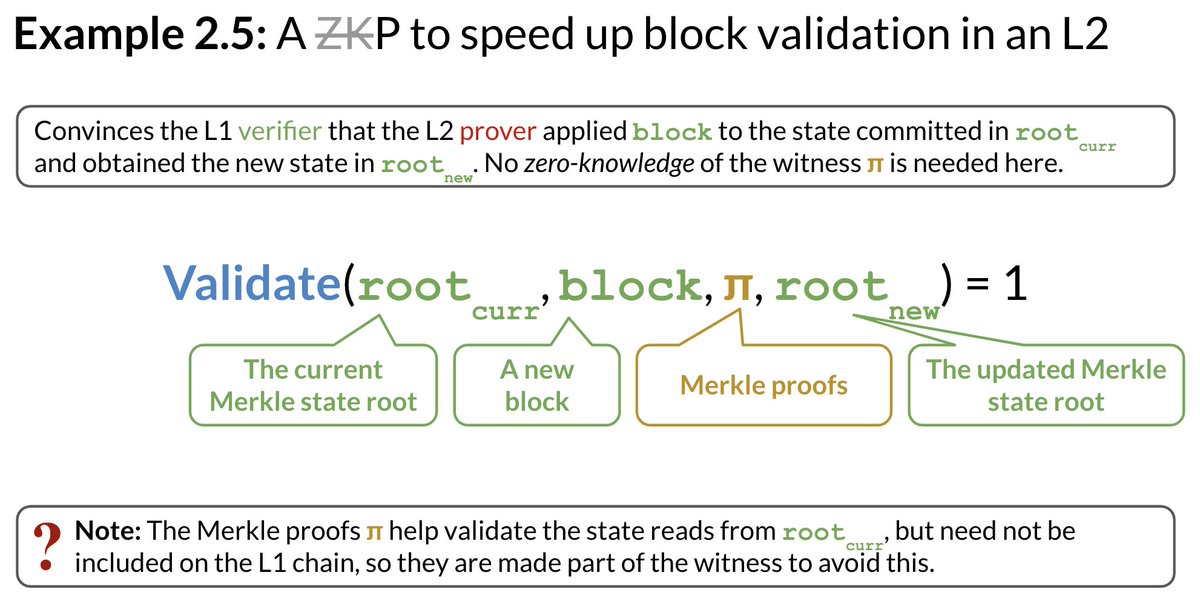
(Note: This is an L2 rollup that cares about data availability, so it stores the L2 TXNs on the L1.)
The L2 *prover* has everything from above (i.e., *x*), plus Merkle proofs for the payers & payees in the block of TXNs (i.e., the witness *w*).
The L1 verifier, will check, via the (non-ZK)P, that the block validation function succeeds on the specified block of payment TXNs, using the Merkle proofs to validate the balances of the payers & update the balances of everyone.
(You can see how such "stateless" validation, based only on the old Merkle root, could work for payments in account-based cryptocurrencies in eprint.iacr.org/2018/968.pdf).
Summary:
(1) ZKPs are the *sane* way of proving something is true, without revealing any unnecessary information.
(2) If you understand that what is being proved is R(x, w) = 1, without leaking w, you understand ZKPs.
(3) Understand (2) via examples: docs.google.com/presentation/d/1b2FoHN983iA_ZkiISMCKa0JqlE40CeqaqNxWjWiJQjE
alin.apt
@alinush407
I put the "crypto" in "cryptocurrency" | Founding Team & Head of Cryptography at @AptosLabs