בשנת 1997 תוכנת המחשב Deep Blue ניצחה את אלוף העולם בשח, גארי קספרוב. ב-#שרשור_תורת_המשחקים הזה נתאר את הגישה האלגוריתמית שעומדת מאחורי Deep Blue ודומיו, ואת הקשר שלה לתורת המשחקים.
משחק השח מט ניתן לתאור כמשחק בצורה רחבה עם ידיעה מלאה. כלומר: שני שחקנים משחקים בתורות, ובכל תור כל שחקן יודע בדיוק מה תהיה תוצאת כל אחת מהפעולות האפשריות שלו (זאת בניגוד, למשל, לשש בש, בו יש גם אלמנט אקראי). בנוסף, משחק השח הוא משחק סכום אפס: ניצחון של האחד פירושו הפסד של האחר.
בפרט, ניתן לתאר את משחק השחמט באמצעות עץ משחק, שבו כל קודקוד מתאר החלטה של אחד השחקנים, הקשתות האפשריות היוצאות מכל קודקוד הן הפעולות האפשריות מהמצב הנתון, והעלים מתארים מצבים בהם המשחק הסתיים. כלומר, כל קודקוד מתאר נצחון של שחקן 1, נצחון של שחקן 2 או תיקו. תמונה להמחשה[1]: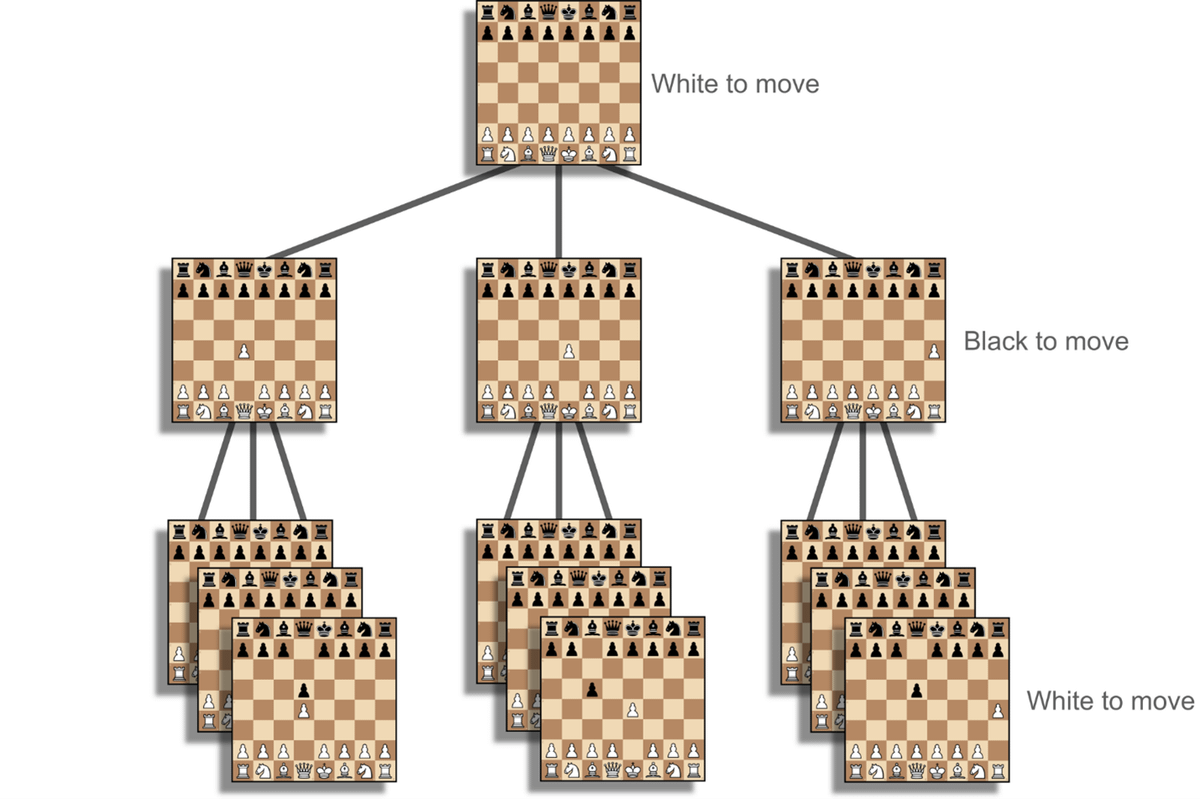
תוצאה ידועה על משחקי סכום אפס אומרת (באופן מעט מפושט) שבכל שיווי משקל במשחק סכום אפס, כל שחקן משחק את האסטרטגיה האופטימלית שלו, כלומר האסטרטגיה אשר מבטיחה לו את התוצאה הטובה ביותר תחת ההנחה שיריבו משחק אופטימלית.
לכן, על מנת למצוא את האסטרטגיה האופטימלית של אחד השחקנים במשחק שח, אפשר לכאורה פשוט לבנות את עץ המשחק ולבצע אינדוקציה לאחור[2], ובכך למצוא שיווי משקל פרפקטי ו"לאמץ" ממנו את האסטרטגיה של השחקן מתאים. נשמע בסך הכל די פשוט, לא?
הגישה הזו יכולה אמנם לעבוד בתאוריה, אבל היא לא פרקטית מבחינה חישובית כיוון שעץ המשחק המלא של משחק השח מט הוא פשוט עצום. בפועל, אפשר לפתוח את עץ המשחק רק עד לעומק מסוים, שיכול להיות רחוק מאוד מהעומק הנדרש על מנת להגיע לסיום המשחק.
הבעיה היא שכאשר מגבילים את עומק העץ בכל שלב, עץ המשחק מסתיים בקודקודים שאינם עלים, כלומר הם מתארים מצבים שבהם המשחק עדיין ממשיך. לכאורה נראה שאי אפשר לבצע אינדוקציה לאחור, כיוון שביצוע אינדוקציה לאחור דורש ידיעה של תוצאת המשחק בעלים. הבעיה הזו נפתרת ע"י שימוש בהיוריסטיקה:
בהינתן עץ משחק חלקי כזה, כלומר עץ שפתחנו עד לעומק מוגבל, נצמיד לכל אחד מהעלים (שהם בד"כ לא באמת עלים בעץ המשחק המלא) תועלות באופן מלאכותי, לפי איזשהו כלל אצבע הגיוני שהוגדר מראש. עלים המתארים לוח שבו יחסי הכוחות הם לטובתנו יקבלו ציון גבוה באופן יחסי, ולהיפך.
כעת נבצע אינדוקציה לאחור לפי הערכים שהגדרנו לעלים בעץ החלקי: בכל קודקוד החלטה שלנו נבחר בפעולה הממקסמת את הערך, ובכל קודקוד החלטה של היריב נבחר בפעולה הממזערת אותו, כיוון שזה מה שאנו מעריכים שהיריב ינסה לעשות (זהו משחק סכום אפס – המטרה של היריב היא שאנחנו נפסיד).
בסופו של דבר, נקפל את העץ אחורה עד שנגיע לקודקוד ההחלטה הנוכחי ונגלה מהי האסטרטגיה האופטימלית (המשוערכת, בגלל השימוש בהיוריסטיקה), ונפעל לפיה. כך ניתן לפתוח בכל תור מחדש עץ משחק שהוא קטן משמעותית מעץ המשחק המלא, ובהינתן היוריסטיקה איכותית ניתן להגיע לתוצאות מעולות.
דוגמא להיוריסטיקה טובה ופשוטה שכזו יכולה להיות סכימה של ציונים שנקבעו לכלי המשחק שעל הלוח, כאשר כלי משחק שלנו יקבלו ציון חיובי וכלי משחק של היריב יקבלו ציון שלילי. למשל: כל רגלי שלנו על הלוח יוסיף 10 נק', רץ שלנו יוסיף עוד 30 נק', רץ של היריב יוריד 30 נק', וכן הלאה[3].
האלגוריתם שתארנו נקרא אלגוריתם ה-Minimax, ואפשר לייעל אותו אפילו יותר ע"י שימוש בטכניקה שנקראת alpha-beta pruning, שבה מתבצע "גיזום" של ענפים מיותרים בעץ המשחק בצורה מתוחכמת[4]. כלומר, זיהוי מראש של מהלכים שבסבירות גבוהה מובילים לתוצאה גרועה והסרה שלהם על מנת לייעל את האלגוריתם.