ב-#שרשור_תורת_המשחקים על שיווי משקל נאש[1] לא הצלחנו למצוא שיווי משקל במשחק הזוג או פרט (מטריצת המשחק מצורפת), והרי הבטחנו שש"מ נאש הוא מושג פתרון שמאפשר לפתור כל משחק. איך ניתן ליישב את הסתירה הזו? האמת היא שהמקור לסתירה הוא בכך שמראש הגבלנו את עצמנו לאסטרטגיות טהורות. נסביר: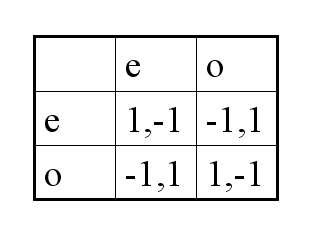
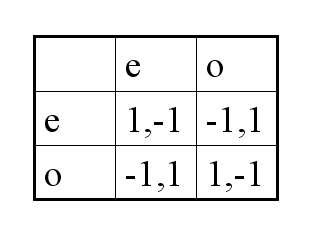
באסטרטגיות טהורות לא תמיד קיים ש"מ נאש. אסטרטגיה טהורה היא אסטרטגיה שבה שחקן בוחר באופן דטרמיניסטי את אחת הפעולות שלו, כלומר הוא בוחר פעולה מסוימת בהסתברות 1. במשחק הזוג או פרט ניסינו למצוא ש"מ שבו כל שחקן בוחר פעולה באופן דטרמיניסטי, אבל בכל פרופיל יש לאחד השחקנים סטייה רווחית:
עבור הפרופילים ("זוג","זוג") ו-("פרט","פרט"), לשחקן הפרט כדאי לשנות את האסטרטגיה שלו, ועבור הפרופילים ("פרט","זוג") ו-("זוג","פרט") לשחקן הזוג כדאי לשנות את האסטרטגיה שלו. כלומר, אף פרופיל אינו מקיים את התכונה שלאף שחקן לא כדאי לסטות לאסטרטגיה אחרת.
אבל מה יקרה אם נרחיב את הדיון לאסטרטגיות מעורבות? אסטטרגיה מעורבת, כפי שניתן לנחש, היא אסטרטגיה שבה שחקן רשאי לבחור באופן אקראי בין מספר פעולות אפשריות. למשל, במשחק הזוג או פרט אסטרטגיה מעורבת שנשמעת די הגיונית תהיה "בהסתברות חצי לשחק זוג ובהסתברות חצי לשחק פרט".
מה קורה כאשר שני השחקנים פועלים לפי האסטרטגיה המעורבת הזו? כעת במקום לדבר על התועלת לכל שחקן, נדבר על *תוחלת* התועלת לכל שחקן, שהיא ממוצע משוקלל של התועלות האפשריות הממושקלות לפי ההסתברות לקבל אותן:
אם כל שחקן בוחר (באופן בלתי תלוי) באקראי בין זוג או פרט, אז בהסתברות רבע נהיה בפרופיל ("זוג","זוג"), בהסתברות רבע נהיה בפרופיל ("פרט","פרט"), בהסתברות רבע נהיה בפרופיל ("פרט","זוג") ובהסתברות רבע נהיה בפרופיל ("זוג","פרט"). לכן, תוחלת התועלת לכל אחד מהשחקנים היא אפס.
נשים לב שכעת לאף שחקן אין סטייה רווחית, למשל עבור שחקן ה"זוג": בהינתן שהשחקן היריב משחק חצי-חצי, אם שחקן ה"זוג" יסטה ללשחק את האסטרטגיה הטהורה "זוג" אז הוא ינצח בהסתברות חצי (וירוויח 1) ויפסיד בהסתברות חצי (וירוויח מינוס 1), כלומר תוחלת התועלת שלו תהיה, שוב, אפס.
כלומר, שחקן ה"זוג" לא יכול לשפר את מצבו, ובאופן דומה גם שחקן ה"פרט", ולכן אנחנו נמצאים בנקודת שיווי משקל! הקטע המעניין הוא שהתופעה הזו אינה מקרית: משפט נאש מבטיח שבכל משחק עם מספר סופי של שחקנים ופעולות קיים לפחות ש"מ נאש אחד (יתכנו יותר) באסטרטגיות מעורבות (יתכן טהורות).
למשפט נאש יש שתי הוכחות יפות: הראשונה משתמשת במשפט נקודת השבת של קאקוטני[2], והשניה פשוטה ואלגנטית יותר ומשתמשת במשפט נקודת השבת של בראוור[3]. עבודות אלה, יחד את תוצאות נוספות בתחום, זיכו את נאש בפרס נובל לכלכלה ב1994.
נסיים בדוגמא למשחק שבו יש יותר משיווי משקל יחיד. המשחק הבא נקרא באופן מסורתי "מלחמת המינים"[4]: במשחק זה כל אחד מבני הזוג צריך לבחור לאיזה בילוי לצאת בערב. באופן די מיזוגני שלא התיישן כ"כ טוב, הגבר מעדיף ללכת לקרב אגרוף בעוד שהאישה מעדיפה ללכת למופע בלט.
למרות העדפותיהם האישיות, בני הזוג מעדיפים לבחור באותו הבילוי מאשר ללכת לבדם לבילוי המועדף עליהם. להלן מטריצת התשלומים (ששוב נלקחה מויקיפדיה) אשר מבטאת העדפות אלה של בני הזוג (הגבר הוא שחקן השורות, והתשלומים שלו כתובים בצד שמאל):

ניתן לראות שהפרופילים ("בלט","בלט") ו-("אגרוף","אגרוף") מהווים שיווי משקל במשחק. אולם, מסתבר שקיים עוד ש"מ מעורב, שבו התועלת לבני הזוג שווה (ולכן אפשר לומר שהוא יותר הוגן): אם כל אחד מבני הזוג בוחר באופציה המועדפת עליו בהסתברות 3/5, אז מסתבר שלאף אחד אין סטייה רווחית!
מקורות:
[1] twitter.com/OmerMadmon/status/1571471728798302209
[2] en.wikipedia.org/wiki/Kakutani_fixed-point_theorem
[3] en.wikipedia.org/wiki/Brouwer_fixed-point_theorem
[4] en.wikipedia.org/wiki/Battle_of_the_sexes_(game_theory)
ההסתברות הנכונה היא כמובן 10/17 ולא 3/5, תודה ל@eyalmarantz5 על התיקון!